2020. 7. 16. 01:18ㆍ선형대수학
PCA란?
: Principal Component Analysis
PCA (주성분 분석)은 많은 데이터가 분포되어 있을 때 이들의 분포된 특성을 나타내는 주 성분을 찾기 위한 방법. 데이터 하나 하나에 대한 성분분석을 하는 것이 아님.

위 <그림 1>과 같이 2차원 평면상에 많은 데이터가 타원형 으로 분포되어 있을 때, 2개의 벡터 ( e1과 e2 ) 로서 이 분포 특 성을 가장 단순하고도 효과적으로 표현. (어느 방향과 크기로 가장 길고, 가장 짧은 지를 나타내는 것) 그래서, 주성분 은 데이터들의 분산(variance) 이 가장 큰 방향을 나타내는 벡터 이다. (변동성이 심한 방향을 지시함) 주성분 e2는 분산이 가장 작은 방향을 나타내는 벡터로서 e1에 대해 수직이다.

<그림 2>와 같이 3차원 데이터의 경우에는 PCA 기법을 이용하여 3개의 서로 수직인 주성분 벡터를 찾을 수 있다.

<그림 3>에서 2차원 좌표평면에 M개의 데이터 (x11, x21), (x21, x22), (x31, x32), ..., (xM1,xM2) 가 예를 들어서 타원형으로 분포되어 있을 때 e1, e2의 방향과 크기를 알면 데이터 분포형태를 파악 가능
기존 Matrix X에서 평균을 빼고 난 후의 데이터 분포를 보니 원점을 중심으로 모이게 되는 것을 볼 수 있습니다.
PCA Calculation Process
Computing PCA using the covariance method
• Step 1 : Organize the data set
• Step 2 : Subtract the mean
• Step 3 : Find the covariance matrix
• Step 4 : Find the eigenvalues and eigenvectors of the covariance matrix
• Step 5 : Transform the data to a new coordinate system
• Step 6 : Deriving the new data set
총 6가지 단계를 거쳐야 합니다.
각 단계를 살펴보도록 합시다.
• Step 1 : Organize the data set
매트랩 코드 :
x1 = [2.5 0.5 2.2 1.9 3.1 2.3 2.0 1.0 1.5 1.1]';
x2 = [2.4 0.7 2.9 2.2 3.0 2.7 1.6 1.1 1.6 0.9]';
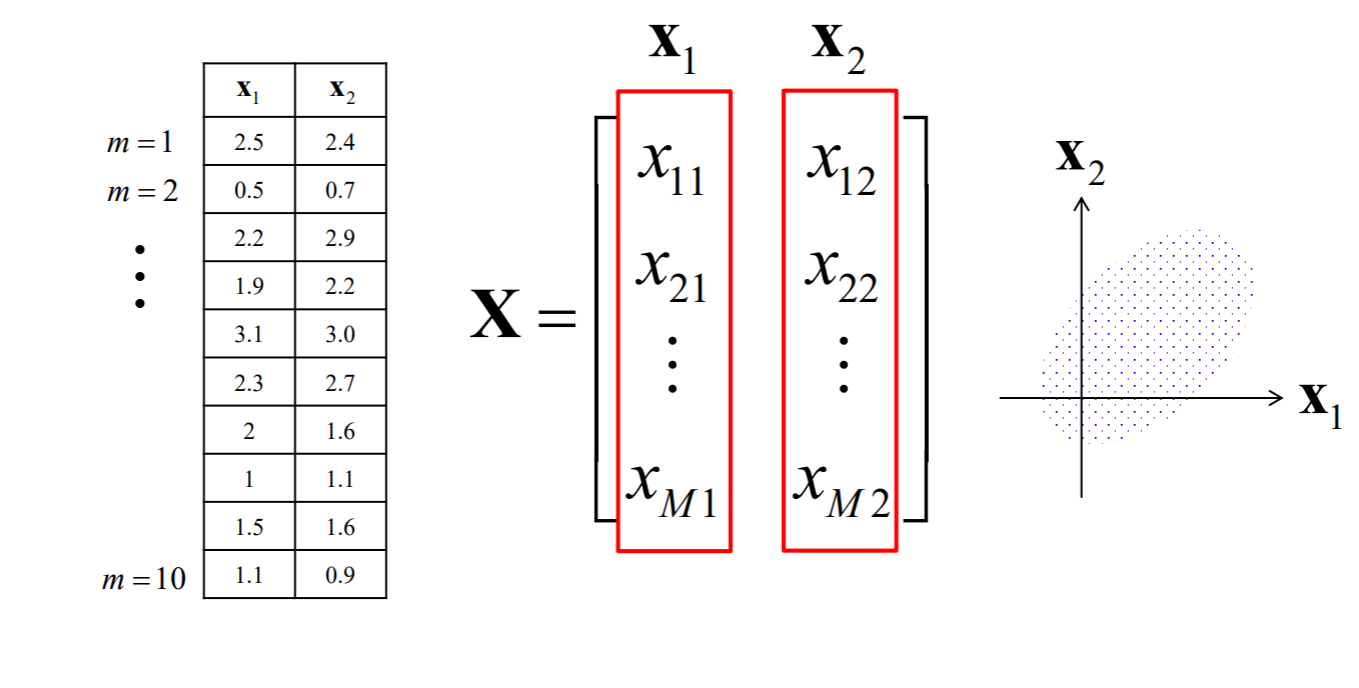
• Step 2 : Subtract the mean
매트랩 코드 :
x1_p = x1 - mean(x1);
x2_p = x2 - mean(x2);

이 과정을 거침으로 데이터셋의 분포가 원점을 중심으로 모이게 됩니다.
figure(1);
plot(x1,x2,'b+');
hold on;
plot([-1 4],[0 0],'k:');
plot([0 0],[-1 4],'k:');
title('Original data');
xlim([-1 4]); ylim([-1 4]);
axis square;
figure(2);
plot(x1_p,x2_p,'b+');
hold on; plot([-1.5 1.5],[0 0],'k:');
plot([0 0],[-1.5 1.5],'k:');
title('Data with the means subtracted');
axis square;
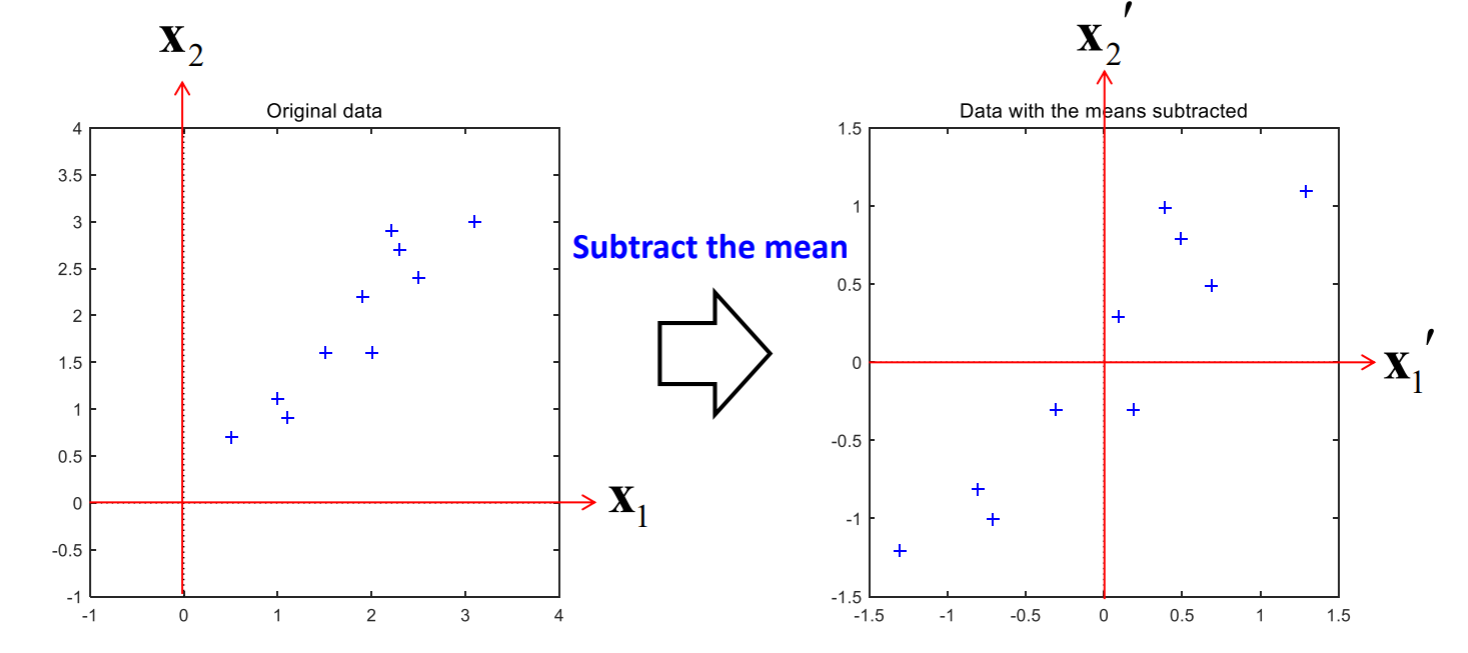
한 눈에 보기에도 데이터가 원점을 중심으로 분포되는 것을 볼 수 있습니다.
• Step 3 : Find the covariance matrix
매트랩 코드 :
X_p = [x1_p x2_p];
C = cov(X_p)
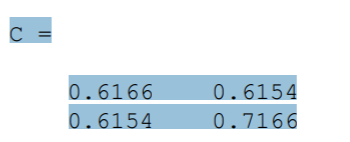
cov 라는 함수를 사용해서 공분산행렬을 찾아줍니다.
[10 X 2] 크기로 이루어진 데이터셋의 공분산 행렬은 [2 X 2] 크기를 갖습니다.

• Step 4 : Find the eigenvalues and eigenvectors of the covariance matrix
매트랩 코드 :
[E, D] = eig(C)

Eigenvalue 크기에 따라 eigenvector를 내림차순으로 정렬합니다.
temp = E(:,1);
E(:,1) = E(:,2);
E(:,2) = temp;
>> E
the most significant eigenvector

The eigenvector with the highest eigenvalue is the principle component of the data set.
매트랩 코드 :
figure(3);
plot(X_p(:,1),X_p(:,2),'b+');
hold on;
plot([-2 2],[0 0],'k:');
plot([0 0],[-2 2],'k:');
plot(X_p(:,1),E(2,1)/E(1,1)*X_p(:,1),'r:');
plot(X_p(:,1),E(2,2)/E(1,2)*X_p(:,1),'r:');
xlim([-2 2]); ylim([-2 2]);
axis square;
다음과 같은 그림이 그려지게 됩니다.

• Step 5 : Transform the data to a new coordinate system
데이터를 새로운 좌표계로 직교 선형 변환(orthogonal linear transformation) 하는 과정
쉽게 말해, 데이터를 회전시킨다고 보면 됩니다.


매트랩 코드 :
Y_all = X_p * E; % two-eigenvectors
Figure(4);
Plot(Y_all(:,1),Y_all(:,2),'b+');
hold on;
plot([-2 2],[0 0],'k:');
plot([0 0],[-2 2],'k:');
xlim([-2 2]); ylim([-2 2]);
title('Data transformed with 2 eigenvectors');
axis square;>>

위 과정은 매트랩의 pca함수로도 동일한 결과를 얻을 수 있습니다. 확인해보세요
매트랩 코드 :
[E,Y_all_func,D] = pca([x1,x2]);

1개의 Eigenvector를 기반으로 새로운 좌표계로 직교 선형 변환 (1차원 데이터로 바뀜)
매트랩 코드 :

y_pca = X_p * e_max;
figure(5);
plot(y_pca,zeros(size(y_pca)),'b+');
hold on;
plot([-2 2],[0 0],'k:');
plot([0 0],[-2 2],'k:');
xlim([-2 2]); ylim([-2 2]);
axis square;

이처럼 1차원 데이터로 바뀌는 것을 확인할 수 있습니다.
• Step 6 : Deriving the new data set
1개의 eigenvector를 이용하여 데이터 변환 후 평균값을 더해 주어 original data 복원함.
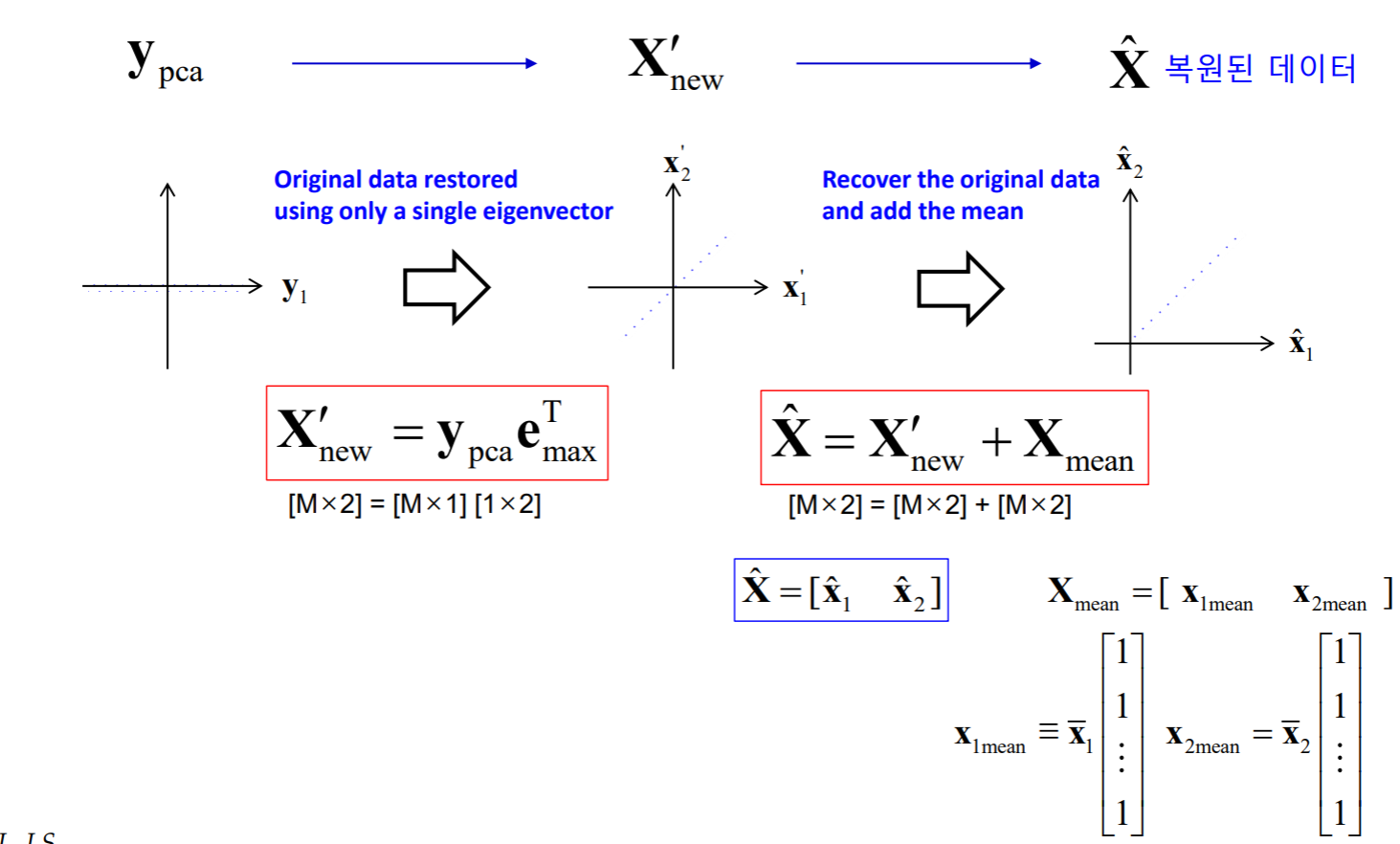
매트랩 코드 :
X_p_new = y_pca * e_max';
x1_mean = mean(x1)*ones(10,1);
x2_mean = mean(x2)*ones(10,1);
x_mean = [x1_mean x2_mean];
X_hat(:,1) = X_p_new(:,1) + x1_mean;
X_hat(:,2) = X_p_new(:,2) + x2_mean;
figure(6);
plot(X_hat(:,1),X_hat(:,2),'b+');
hold on;
plot([-1 4],[0 0],'k:');
plot([0 0],[-1 4],'k:');
xlim([-1 4]); ylim([-1 4]);
axis square;
title('Original data restored using only a single eigenvector');
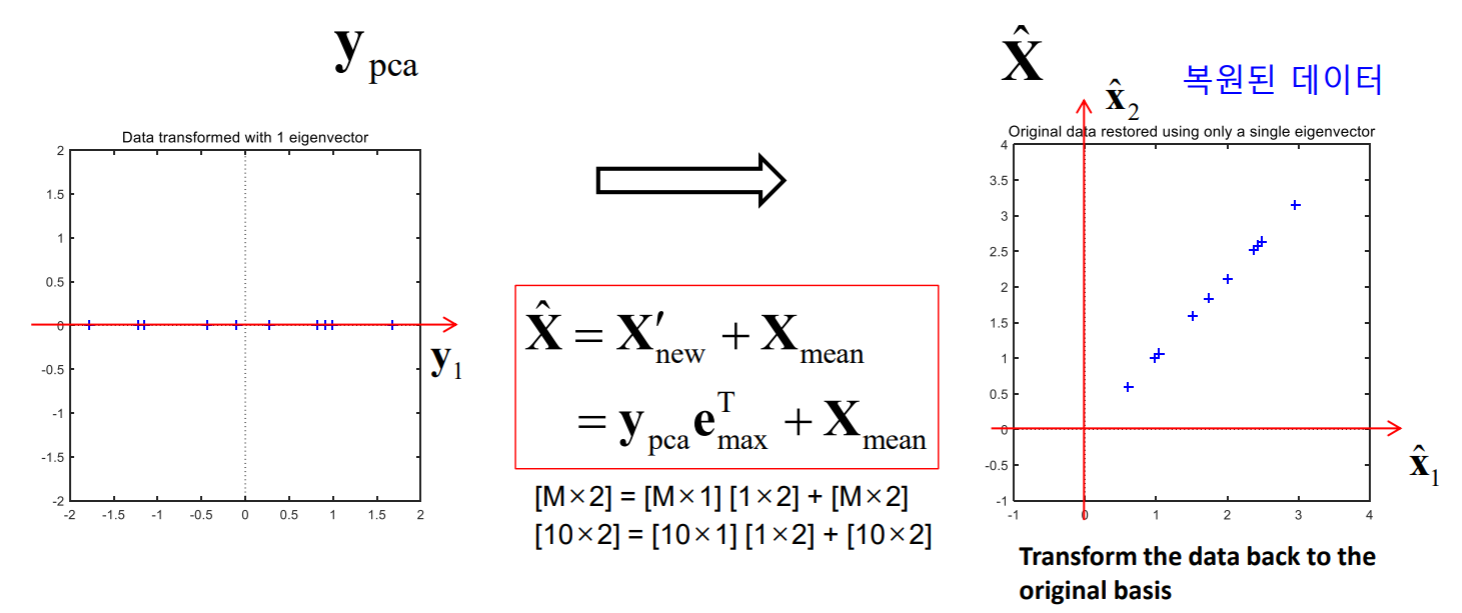
최종적으로 6가지 단계를 거치면 다시 복원된 데이터를 가질 수 있습니다.
그럼, PCA를 이용해 Face Recognition을 해봅시다.
1. PCA를 이용한 얼굴인식 알고리즘 개념
• PCA기법을 이용해 인식 대상의 얼굴 중 입력 얼굴이 누구의 얼굴인지를 인식 (ex. 보안시스템)
• 학습 단계와 인식 단계로 구분 인식 대상의 얼굴 이미지(학습 이미지, 여러 명)로부터 Database를 구축하는 학습 단계


2. PCA 얼굴 인식
Ex) 가장 큰 2개의 Eigenvalue에 해당하는 Eigenvector 2개를 기반

– 이미지 불러오기
매트랩 코드 :
%% 학습 이미지 불러오기
S = []; % 학습 이미지 저장 행렬
M = 25; % 학습 이미지의 개수
icol = 92;
irow = 112;
N = icol*irow; %학습 이미지의 차원(pixel 개수)
for i = 1:M
img = imread([‘database\training\' num2str(i,'%03g')
'.bmp']);
temp = reshape(img', N, 1); % 1차원 벡터로 만든다.
[N x 1]
temp = double(temp);
S = [S temp];
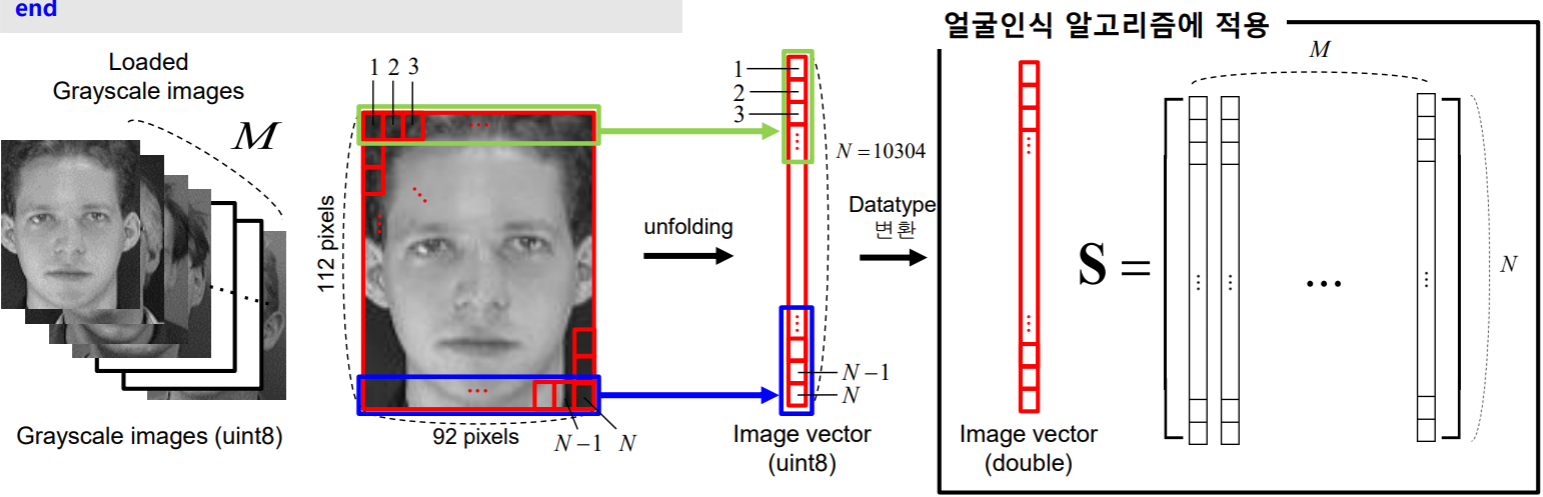
end 여기서 M개의 grayscale 이미지는 uint8(unsigned integer 8-bit)이며 0, 1, …, 255의 값으로 명암을 표현
이미지를 얼굴인식 알고리즘에 적용하기 위하여 데이터타입 변환 112 x 92 pixels의 matrix를 10304 x 1 의 vector로 변환 (unfolding) Datatype을 uint8에서 double로 변환
– 이미지 정규화
학습이미지의 픽셀 값 분포를 일정하게 하기 위함.
학습 이미지가 평균(m)이 128, 표준편차(s)가 128인 정규분포를 따르도록 함으로써 빛과 배경에 의한 인식 오류를 줄임
매트랩 코드 :
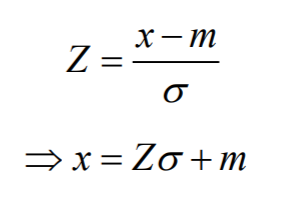
%% 이미지 정규화
X = zeros(N, M);
for i = 1:M
temp = S(:,i);
m = mean(temp);
st = std(temp);
Z = (temp - m) / st; % Standard normal distribution
X(:,i) = Z * 128 + 128; % S = 128 + (128 * Z) -> N(128,128)
end
